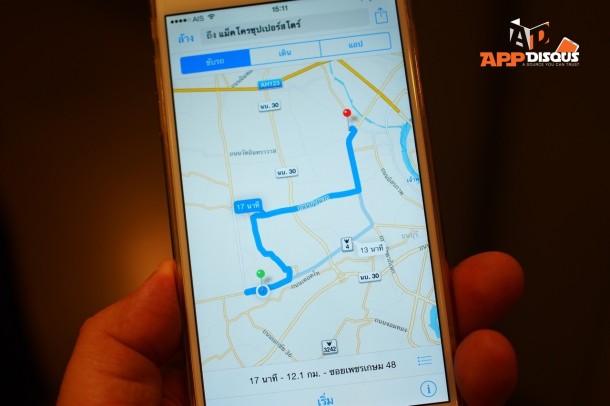
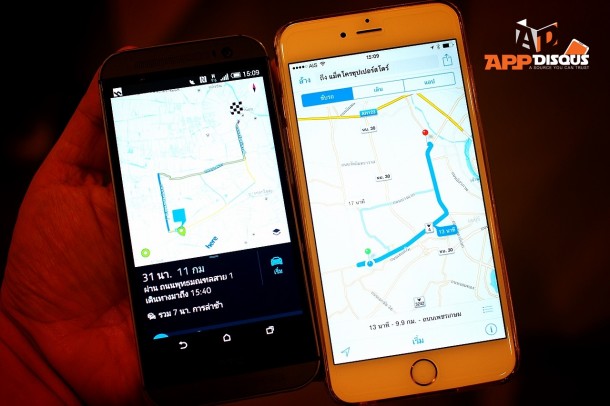
เคยสงสัยกันไหมครับ? ว่าเวลาเราต้องการเดินทางจากตำแหน่งใดตำแหน่งหนึ่งไปยังจุดหมายปลายทาง เราค้นหาเส้นทางจากระบบแผนที่ไม่ว่าจะเป็น Google Maps, Here Maps หรือ Apple Maps แล้วมันก็คำนวณเส้นทาง สุดท้ายก็เลือกหรือเสนอเส้นทางให้กับเรา ซึ่งเราเชื่อว่ามันเป็นเส้นทางที่ดีที่สุด … มันจริงไหมนะ? และมันทำได้อย่างไร?
หลายคนก็คงตอบแบบกำปั้นทุบดินว่า “มันก็ใช้โปรแกรมคำนวณสิ!!” เอ่อ…. คือ มันก็ใช่นะ แต่มันแทบไม่ได้ประโยชน์อะไรจากคำตอบนั้นเลย หากเราต้องการประโยชน์หรือความรู้จากมัน เราก็ต้องคิดไปให้ลึกและไกลกว่านั้นครับ นั่นคือ โปรแกรมที่ว่ามันใช้อะไรมาคำนวณหรือตัดสินใจ? บทความนี้มีคำตอบให้ครับ และเราสามารถคำนวณมือ โดยไม่อาศัยโปรแกรมได้ด้วยนะครับ มาลองกันดูดีกว่า …
ในบทความนี้
การเปลี่ยนระบบแผนที่ให้กลายเป็นโมเดลปัญหา
สำหรับการหาเส้นทางที่สั้นที่สุดนั้น วิธีการที่เป็นที่นิยมมากที่สุดก็คือ การสร้างแบบจำลองเส้นทางหรือแผนที่เป็นโมเดลทางคณิตศาสตร์ที่เรียกว่า “กราฟ(Graph)” ซึ่งเจ้ากราฟนี้ประกอบด้วย จุด(Vertex) และ เส้น(Edge) ซึ่ง จุด จะใช้แทนทางแยก สถานที่ หรือตำแหน่งอ้างอิงอื่นๆ ส่วน เส้น จะใช้แทนถนน จากนั้นค่อยนำกราฟที่เป็นตัวแทนระบบแผนที่ไปคำนวณหาเส้นทางที่สั้นที่สุด
ตัวอย่างกราฟอย่างง่าย
รูปภาพ 1: กราฟที่มี 2 จุด และ 1 เส้น
รูปภาพ 2: กราฟที่มี 4 จุด และ 3 เส้น
รูปภาพ 3: กราฟที่เป็น Cycle
ตัวอย่างข้างต้นเป็นกราฟที่ง่ายที่สุด ที่เขาเรียกว่า Simple Graphs แต่เมื่อเปลี่ยนระบบแผนที่มาเป็นกราฟ เราจะได้กราฟที่มีความซับซ้อนมากขึ้น มีทั้งกราฟที่เป็นลูป(แทนถนนที่วนมาที่จุดเดิมโดยไม่ผ่านแยกใดๆ) Multiple Graph(จุดสองจุดมีถนนเชื่อมกันมากกว่า 1 เส้น) กราฟระบุเส้นทางเข้ามาด้วย ส่วนใหญ่จะเป็นกราฟทางเดียวหรือกราฟตรง(แทนถนนที่เป็นวันเวย์) มันทำให้โครงสร้างใหญ่และมีความซับซ้อนมากขึ้น
รูปภาพ 4: ตัวอย่างกราฟที่มีความซับซ้อนมากขึ้น
หมายเหตุ: นักคอมพิวเตอร์หรือกลุ่มเทคโนโลยีสารสนเทศจะเรียก จุด ว่า โหนด(Node) และเรียก เส้น ว่า อาร์ค(Arc)
การหาเส้นทางที่สั้นที่สุด?
เมื่อเราต้องการหาเส้นทางที่สั้นที่สุด บางโมเดลของปัญหาอาจสนใจแค่ว่า เราจะผ่านจุดหรือแยกให้น้อยที่สุดได้อย่างไร? ตัวอย่างเช่น
รูปภาพ 5: เส้นทางจาก A ไป C ต้องผ่าน B เท่านั้น(ไม่มีเส้นทางอื่น)
รูปภาพ 6: กราฟที่ระบุค่าถ่างน้ำหนักเข้ามาด้วย เส้นทางจาก A ไป C ที่สั้นที่สุดระยะทางเป็น 4
รูปภาพ 7: กราฟที่ระบุค่าถ่างน้ำหนักเข้ามาด้วย เส้นทางจาก A ไป E ที่สั้นที่สุดต้องผ่าน B ระยะทางเป็น 12
แต่เมื่อนำมาโมเดลปัญหามาใช้ในชีวิตจริงเราจะพบว่า การหาเส้นทางที่ดีหรือสั้นที่สุดนั้น มันไม่ได้นับที่จำนวนแยกเลย เชื่อว่าเพื่อนๆ คงมองออกว่าสิ่งที่ทำให้เราเสียเวลาบนท้องถนนมากที่สุด ก็คือ รถติด + ระยะทาง + ด่าน + อุบัติเหตุ และอื่นๆ อีกมากมาย (เราเรียกว่าค่าถ่วงน้ำหนัก) ดังนั้น การแก้ปัญหาที่แท้จริง เราจึงได้ทำการเพิ่มค่าถ่วงน้ำหนักให้กับเส้นทางของกราฟ ซึ่งค่าถ่วงน้ำหนักตัวนี้แล้วแต่ว่าเจ้าไหนจะเอาอะไรมาคิดบ้าง? ซึ่งมันจะส่งผลต่อประสิทธิภาพของระบบแผนที่นั่นเอง นี่ก็เป็นตัวชี้วัดอีกอย่างหนึ่งว่าใครที่เก่งในการจัดการค่าถ่วงน้ำหนักก็จะทำให้ระบบแผนที่มีประสิทธิภาพมากกว่า
จากนั้นเมื่อเราแทนปัญหาด้วย จุด เส้น ค่าถ่วงน้ำหนัก และระบุทิศทางของเส้นทางเรียบร้อยแล้ว เราก็จะใช้โปรแกรมที่รันด้วยอัลกอริทึมเฉพาะตัวมาหาผลเฉลยหรือเส้นทางที่ดีที่สุดได้ ซึ่งเจ้าอัลกอริทึมตัวนี้ ระบบแผนที่แต่ละเจ้า ทั้ง Google Maps หรือ Here Maps และอื่นๆ จะใช้อัลกอริทึมที่แตกต่างกัน ที่ไม่ยอมเผยความลับให้ใครรู้ได้ง่ายๆ … แต่ว่าโดยทั่วไปแล้ว การหาเส้นทางที่สั้นที่สุดจะนิยมใช้อัลกอริทึมพื้นฐานเดียวกัน นั่นคือ อัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm) แล้วนำไปปรับปรุงเปลี่ยนแปลงให้มันตรงกับความเป็นจริงมากที่สุด หรือ ใส่ค่าถ่วงน้ำหนักที่ครบถ้วนและเหมาะสมก็จะทำให้การคำนวณมีประสิทธิภาพมากขึ้น อย่างไรก็ตามก็มีอัลกอริทึมอื่นๆ อีกที่ได้รับความนิยมมากเช่นกัน ณ ที่นี้ เราจะนำเสนอให้เพื่อนๆ ได้รู้จัก 2 อัลกอริทึม ที่สำคัญ ที่แตกต่างกันมาก และให้ผลเฉลยที่ต่างกันมากเช่นกัน แต่กลับมีความนิยมไม่แพ้กันเลยครับ ได้แก่ อัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm) และ ระบบมด (Ant System)
อัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm)
Dijkstra’s algorithm ถูกคิดค้นขึ้นโดยนักวิทยาการคอมพิวเตอร์ชาวดัตช์นามว่า แอ็ดส์เคอร์ ไดก์สตรา(Edsger Dijkstra) ในปี 1959 เพื่อแก้ไขปัญหาการหาเส้นทางที่สั้นที่สุดจากจุดหนึ่งใดๆ สำหรับกราฟที่มีความยาวของเส้นเชื่อมไม่เป็นลบ สำหรับขั้นตอนวิธี Dijkstra’s Algorithm นี้จะหาระยะทางสั้นที่สุดจากจุดหนึ่งไปยังจุดใด ๆ ในกราฟโดยจะหาเส้นทางที่สั้นที่สุดไปทีละจุดยอดเรื่อยๆ จนครบตามที่ต้องการ
Dijkstra’s algorithm
กำหนดให้จุด จุดหนึ่งภายในกราฟเป็นจุดเริ่มต้น (initial node) และกำหนดให้ “ระยะทางของจุด X” (distance of node X) หมายถึงระยะทางจากจุดเริ่มต้นไปยังจุด X ใด โดย Dijkstra’s algorithm จะกำหนดค่าระยะทางเริ่มต้นไว้บางจุดและจะเพิ่มค่าไปทีละขั้นตอน
- กำหนดให้ทุกจุดมีค่าระยะทางตามเส้นเชื่อม โดยให้จุดเริ่มต้นมีค่าเป็นศูนย์ และจุดอื่นๆมีค่าเป็นอนันต์
- ทำเครื่องหมายทุกจุด ยกเว้นจุดเริ่มต้นว่ายังไม่ไปเยือน (unvisited) ตั้งให้จุดเริ่มต้นเป็นจุดปัจจุบัน
สร้างเซตของจุดที่ยังไม่ไปเยือนขึ้นมาเซตหนึ่งซึ่งประกอบด้วยจุดทุกจุด ยกเว้นจุดเริ่มต้น - จากจุดปัจจุบัน พิจารณาจุดข้างเคียงตามเส้นเชื่อมทุกจุดที่ยังไม่ไปเยือน และคำนวณระยะทางต่อเนื่องของเส้นเชื่อม ตัวอย่างเช่น ถ้าจุดปัจจุบันคือ A มีระยะทางของจุดเป็น 6 และเส้นเชื่อมที่ต่อจาก A ไปยังจุดข้างเคียง B มีระยะทางเป็น 2 ดังนั้นระยะทางของจุด B (โดยผ่าน A) จึงเท่ากับ 6+2=8 เป็นต้น ถ้าระยะทางที่คำนวณได้มีค่าน้อยกว่าค่าระยะทางที่บันทึกอยู่ของจุดนั้น ให้เขียนทับค่าระยะทางของจุดดังกล่าว แม้ว่าจุดข้างเคียงได้ถูกพิจารณาแล้ว แต่ก็ยังไม่ทำเครื่องหมายว่าไปเยือนแล้ว (visited) ในขั้นตอนนี้ จุดข้างเคียงจะยังคงอยู่ในเซตของจุดที่ยังไม่ไปเยือนเช่นเดิม
- เมื่อพิจารณาจุดข้างเคียงจากจุดปัจจุบันครบทุกจุดแล้ว ทำเครื่องหมายที่จุดปัจจุบันว่าไปเยือนแล้ว (visited) และนำออกจากเซตของจุดที่ยังไม่ไปเยือน โดยจุดที่ไปเยือนแล้วนี้จะไม่ถูกนำมาตรวจสอบอีก ค่าระยะทางที่บันทึกอยู่จะสิ้นสุดและมีค่าน้อยที่สุด
- จุดปัจจุบันตัวถัดไปที่ถูกเลือกจะเป็นจุดที่มีค่าระยะทางน้อยสุดในเซตของจุดที่ยังไม่ไปเยือน
- ถ้าเซตของจุดที่ยังไม่ไปเยือนว่างแล้วให้หยุดการทำงาน ขั้นตอนวิธีเสร็จสิ้น แต่ถ้าหากไม่ใช่ให้เลือกจุดที่ยังไม่ไปเยือนที่มีค่าระยะทางน้อยสุดเป็นจุดปัจจุบัน แล้ววนกลับไปทำขั้นตอนที่ 3
รูปภาพ 8: รูปภาพแสดงการใช้ Dijkstra’s algorithm
โค๊ดภาษา C++ สำหรับ Dijkstra’s algorithm(คลิกที่รูป)
ระบบมด (Ant System)
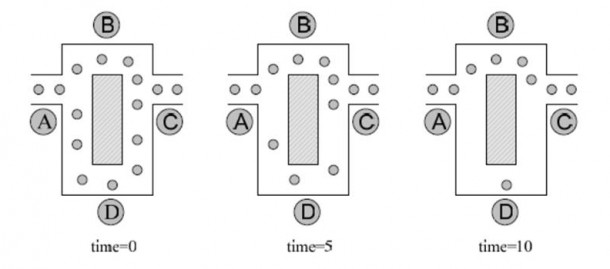
อัลกอริทึมของระบบมด(Ant Colony Algorithm) เป็นอัลกอริทึมที่จำลองหรือได้แนวคิดมาจากการเดินหาอาหารของมด โดยมดจะอาศัยสารเคมีที่เรียกวาฟีโรโมน (Pheromone) ที่มดแต่ละตัวก่อนหน้านี้ปล่อยลงบนพื้นและเมื่อมดตัวหลังเดินตามมาก็จะปรับปรุงฟีโรโมนลงไปบนพื้นอีก ซึ่งเหตุนี้เองฟีโรโมนจึงเป็นข้อมูลที่สําคัญในการหาเส้นทางจากแหล่งอาหารกลับไปยังรัง ซึ่งอธิบายพฤติกรรมของมดโดยใช้ข้อมูเรื่องปริมาณของฟีโรโมนในการหาเส้นทางเดินจากรังไปยังแหล่งอาหาร
รูปภาพ 9: รูปภาพแสดงวิธีการเดินของมด
จุดเด่นของระบบมด ก็คือ เป็นขั้นตอนวิธีที่สามารถหาผลเฉลยได้มากกว่า 1คําตอบ ทําให้ได้เส้นทางที่หลากหลาย เมื่อเส้นทางที่เหมาะสมที่สุดเกิดมีปัญหา เช่น เนื่องจากเส้นทางชำรุด หรือการจราจรหนาแน่นจะสามารถรู้ว่าเส้นทางที่เหมาะสมเส้นรองต่อไปคือเส้นทางใด โดยที่ไม่ต้องทำาการคำนวณหาอีกครั้ง
ข้อแตกต่างของ อัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm) และ ระบบมด (Ant System) ก็คือ อัลกอริทึมของไดก์สตรา จะได้เพียงคำตอบเดียว แต่ได้เส้นทางที่สั้นที่สุด ส่วนระบบมด จะได้หลายคำตอบ แต่อาจไม่ใช่เส้นทางที่สั้นที่สุด นี่คือตัวอย่างการทดลองของอัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm) และ ระบบมด (Ant System) บนระบบแผนที่จำลอง โดย ราชการ ปรึกษาดี และ สุนันฑา สดสี ในบทความเรื่อง การเปรียบเทียบหาเส้นทางที่เหมาะสมโดยวิธีระบบมดและ Dijkstra’s Algorithm แสดงผลการทดลองดังกราฟ
รูปภาพ 10: รูปภาพแสดงผลการเปรียบเทียบ อัลกอริทึมของไดก์สตรา(Dijkstra’s algorithm) และ ระบบมด (Ant System)
สำหรับการนำไปใช้ในระบบแผนที่ทั้ง Google Maps, Here Maps, Apple Maps หรืออื่นๆ นั้นก็จะประยุกต์เอาอัลกอริทึมเหล่านี้นี่หละครับไปใช้ อาจไม่ได้ใช้อัลกอริทึมเดียว อาจมีการปรับแต่ง ปรับแล้วปรับอีก เพื่อเพิ่มประสิทธิภาพสำหรับแข่งขันในตลาด พวกเราอาจเคยได้ยิน Apple ออกมาบอกว่า Apple Maps ยิ่งมีคนใช้เยอะก็ยิ่งมีประสิทธิภาพมากขึ้น นั่นแสดงว่า อัลกอริทึมของ Apple Maps อาจทำงานบนพื้นฐานวิธีระบบมดก็เป็นได้ ส่วน Google Maps ที่เราเคยค้นหาเส้นทาง บางทีก็ได้เส้นทางเดียว(Dijkstra’s Algorithm) บางครั้งก็มีเส้นทางสำรองให้เราเลือก(ระบบมด) แสดงว่าอาจมีการผสมผสานทั้งสองอัลกอริทึมก็เป็นได้ และแผนที่บางตัวจะมีให้เราติ๊กเลือกได้เลยว่า ต้องการเส้นทางสำรองหรือไม่ นั่นแปลว่า ถ้าเราไม่ต้องการอาจคำนวจด้วย Dijkstra’s Algorithm แล้วได้เส้นทางที่ดีที่สุด แต่เมื่อติ๊กเลือกขอเส้นทางสำรองด้วย เราอาจได้เส้นทางที่ไม่ได้ดีที่สุดเลยก็เป็นได้ครับ
แหล่งอ้างอิง:
1. http://waynewbishop.com/swift/graphs/dijkstra/
2. http://hastuts.com/dijkstra-shortest-path-algorithm-in-cpp/
3. https://www.youtube.com/watch?v=UG7VmPWkJmA
4. http://202.44.34.144/nccitedoc/admin/nccit_files/NCCIT-2011040226.pdf
5. http://202.44.34.144/nccitedoc/admin/nccit_files/NCCIT-2011080300.pdf
6. https://mikecvet.wordpress.com/2011/01/27/linkedin-maps-your-professional-network-as-a-pretty-graph/